The Misnamed Doctrine

I went skiing last weekend on the hills surrounding a local set of football and soccer fields with a friend. It was around 20 degrees F outside, and the snow was icy and fast, which more than made up for the thin cover. Here are some of the lines we took:

The top line that crosses the road allows for a nice little jump as you cross the road, with a relatively comfortable & steep landing. We didn’t manage to get much air there on account of the snow cover being thin. In icier conditions it should be possible to really send it off of that road!

The middle line goes through a gate and has a second drop down to the lower field.

The third line typically is the sledding hill that kids use on snow days.

It took roughly 60 min for us to become physically exhausted from walking up and down the hills with our skis, but we both agreed that the experience, overall, definitely felt like “skiing.”

ChatGPT does not display any ads alongside or inside of its responses. Here is an example:

Great answers! They are not that different in terms of content from my non-ad-blocked experience inside of google search — showers, dry heat, scratching, lotions — seems like many of the same bases are covered, with Google a little more rough around the edges, but with no notable ads displayed in the first few search results, to their credit:

To get prose, you have to click into a link — “Vistadermsa” seems like it is someone’s business so let’s look at the second, more generic sounding “Healthline”:

INFINITI! NY PRESBYTERIAN! These ads took like 3 seconds to load and totally ruined my experience. Chalk one up for ChatGPT.

With Sam Altman simultaneously spiking the football on its rapid adoption and its intensive compute cost I think we should all take a deep breath and ask ourselves the following questions:

• How much of our collective delight with ChatGPT is attributable to it being an ad-free version of google search?
• What would an ad-supported version of ChatGPT look like?
• Do ads make an AI experience feel “less intelligent?”
• What would a “native ad” experience be inside of ChatGPT and how is it different from outright misinformation?

Definitions

There are many recent news articles that discuss post-pandemic office reopening plans:

• https://www.bloomberg.com/news/articles/2021-06-14/wall-street-s-return-to-office-divide-laid-bare-by-goldman-citi
• https://www.cnn.com/2021/05/05/tech/google-office-remote-work-pandemic/index.html
• https://www.cnn.com/2021/04/14/tech/uber-office-return-employees/index.html

One topic that seems to be missing in the current reopening discourse is how reopening an office should depend on the type of work that is done at the office. Here are four very very broad categories of work that can happen at offices:

1. Internal-infrastructure work

2. Internal-creation work

3. Internal-collaboration work

4. External-collaboration work

The decision to reopen should be based on the extent to which each of these types of work is necessary to a particular firm. Some types of work are impacted heavily by being able to do in-person work, others are not. Let’s define each type:

Internal-infrastructure work is dominated by tasks that require the worker to touch property owned or controlled by the firm. Examples include operation of factory equipment, maintenance of on-premise IT infrastructure, testing and design of physical products, and janitorial work. This work cannot be done remotely. Note that external infrastructure work is somewhat irrelevant to the question to reopen an office. Work that requires employees to view/edit highly confidential or sensitive information can also be added to this category, as the physical security of the location where the viewing/editing is happening is largely an infrastructure question.

Internal-creation work is knowledge work that is done in isolation by employees. Examples of this include creating/modifying documents, creating/modifying spreadsheets, writing computer software, and creating/modifying presentations.

Internal-collaboration work is dominated by tasks that require communication among members of the firm. Examples of this type of work include synchronous and asynchronous communication tasks — meetings, emails, electronic chats, informal hallway chats, one-on-one meetings, etc.

External-collaboration work is typically done in a sales or customer support capacity. The work is dominated by a need to communicate with external parties to the firm in a way that pleases. Pleasing non-customers results in sales, pleasing existing customers reduces customer churn. This category can also be applied to non-sales-but-external functions such as recruiting, where, for example, prospective employees can be viewed as a type of customer.

This post will focus on quantifying the impact of reopening an office on external-collaboration work.

Quantitative Analysis

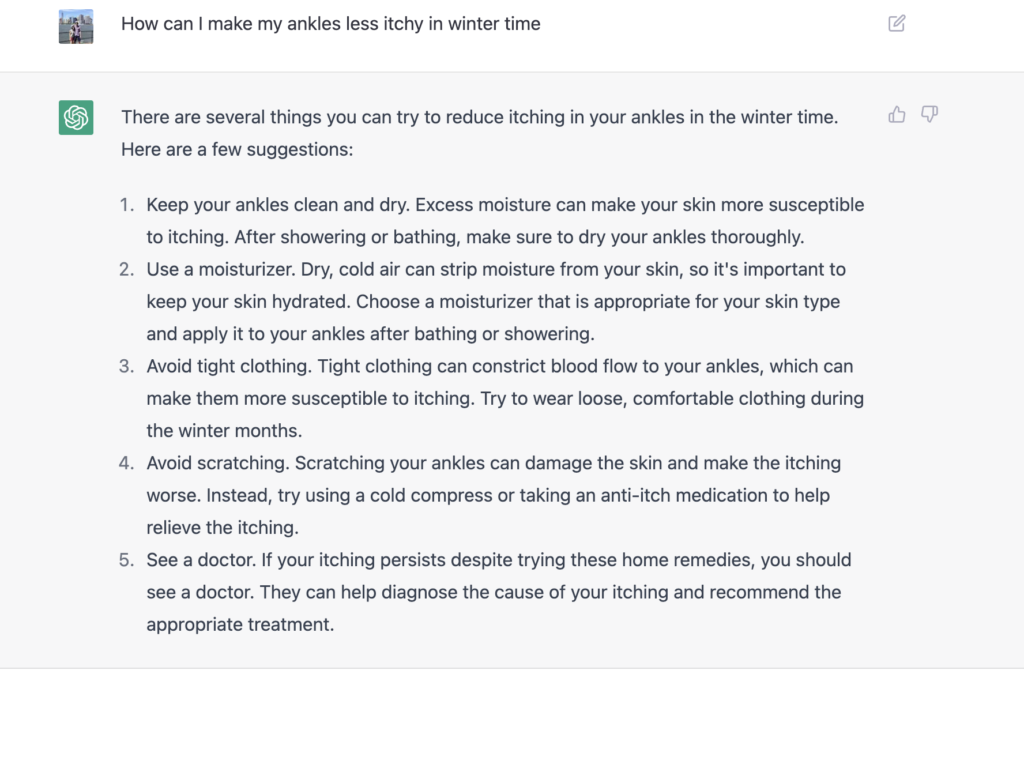
Do business trips increase sales? Do customer meetings at a Very Nice Office result in better win rates? The answer is “it depends.” More specifically, “it depends on the percentage of your customers that are willing to interface in-person.”

Intuitively it may seem obvious, but it is a question that can be modeled and answered quantitatively. Specifically, win-rate investments in things such as business trips and in-person events (which also require in-person reciprocity from the customer) will have their overall impact bound by the overall extent to which those customers have returned to in-person operations.

Mathematically, we can define our sales velocity for a given strategy (remote, in-person) SV_strategy to be equal to the product of the probability of a given sales rep from the team winning a sale, based on their skills alone, the volume or size of the sales team using that strategy, and the probability that the strategy “matches” a given prospect from the marketplace:

SV_strategy = P(win_strategy) · vol_strategy · P(match_strategy)

Note that there is an implicit time value of unity in this rate expression. The notion of a “match” here is intended to reflect that in-person sales only work when both the customer and the sales rep meet in-person.

If we make the (strong) assumption that the market bifurcates into two non-overlapping sets — customers that only take meetings remotely and customers that only take meetings in-person, we can say that in-person sales teams will take market share when:

SV_in-person > SV_remote

I.e. when:

P(win_in-person) · vol_in-person · P(match_in-person) > P(win_remote) · vol_remote · P(match_remote)

If we then note that in-person “outside” sales teams are typically more expensive to run than remote “inside” sales teams, with in-person teams making up in additional win-rate with what they lack in size, we can then assume, roughly:

P(win_in-person) · vol_in-person ≈ P(win_remote) · vol_remote

An example of this assumption: a 20-member inside sales team with a win-rate of 10% can roughly be compared with a 10-member outside sales team with a win-rate of 20%. So if we assume all of that, we are left with an in-person-sales strategy taking market share from remote sales when:

P(match_in-person) > P(match_remote)

Oversimplified: remote sales strategies will continue to take market share as long as the market is predominantly operating remotely.

The above analysis assumes a lot. For example, it doesn’t consider the possibility that a sales team could have the option to handle a sale either remotely or in-person. Nor does it consider the very-real-world notion of a shootout, where sales teams compete in the same marketplace. And I am too lazy to write down conditional probability expressions tonight.

Simulation

To model these scenarios (and the probability of a in-person sale conditioned on the probability that the prospective customer operates in-person), we proceed with a simulation. Suppose you are the head of sales at a small firm that competes within a larger universe of firms. You have 20 sales people on your team. Your competitors, in sum, total 100 sales people. Your market consists of 1000 customers that are not quite operating at pre-pandemic levels, in terms of willingness to do deals in-person. Say they are operating 40% in-person. Customers that are open to in-person deals can also do sales deals remotely.

You, the head of sales, have two levers at your disposal — you can invest in in-person trips and events to really focus on those 40% of customers that are receptive to in-person interactions, thereby increasing your win rate with those customers, or you can invest in growing the effective size of your sales team  (by hiring more, investing in online chat or video-conferencing tools that expand their reach, etc. etc.).

Assuming that the baseline remote-only win rate is 10%, we can run a monte carlo simulation that compares the results of increasing the 20-person team’s win rate for in-person deals progressively, with a strategy that increases the size of the 20-person team (either by hiring or investing in remote work technology adoption). A monte carlo simulation is an alternative approach to solving for the end-result of a probabilistic process when it is too complicated to model all aspects of the process. Here we are using it because we are too lazy to write down and solve equations that model a sales team that can handle in-person or remote sales in a competitive environment.

We first assume that the percentage of the customer base that is receptive to in-person sales stays constant at 40%.

ON EVERY CHART THAT FOLLOWS, THE Y-AXIS REPRESENTS MARKET SHARE, RANGING FROM 0.0 TO 1.0 AND THE X-AXIS IS TIME.

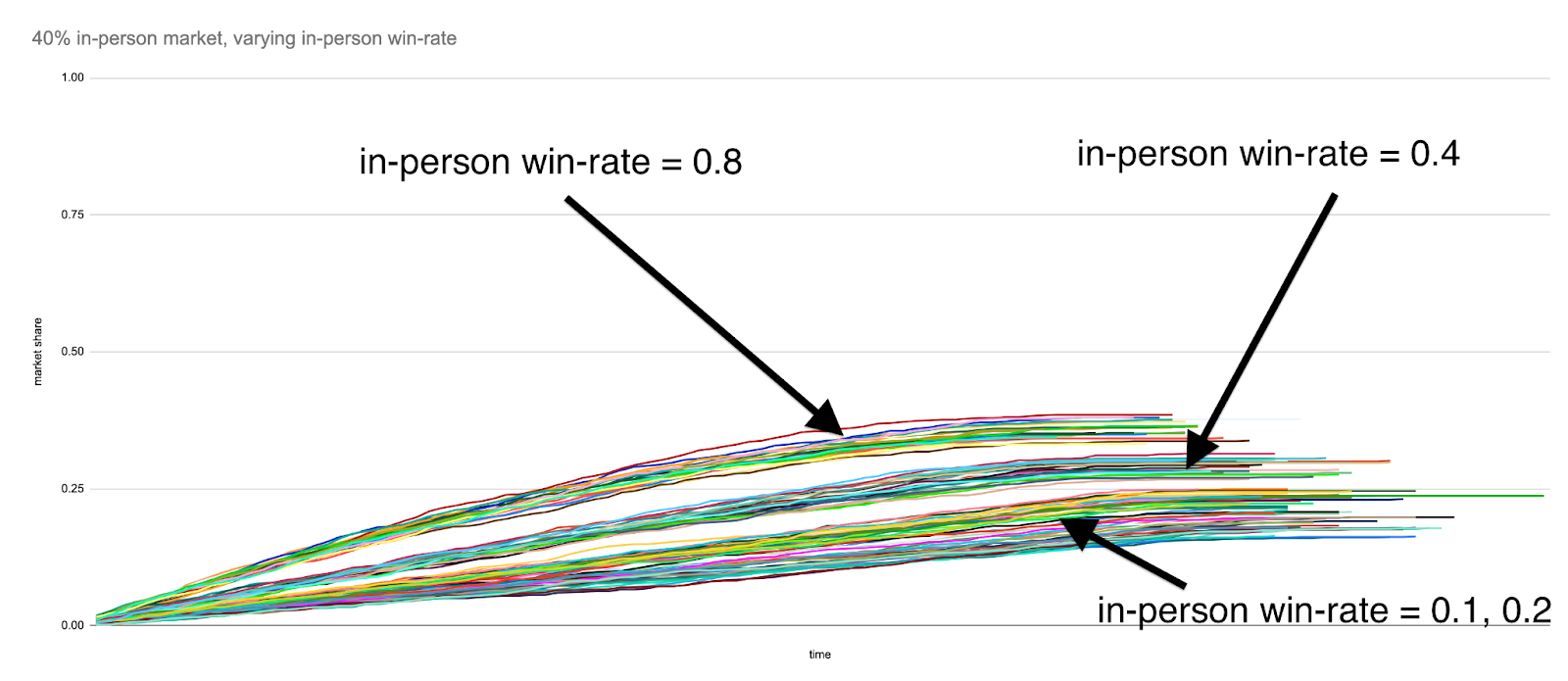
Here are the results when we examine in-person win-rates of 0.1, 0.2, 0.4 and 0.8:

And here are the results when we successively double the team size — 20, 40, 80, 160:

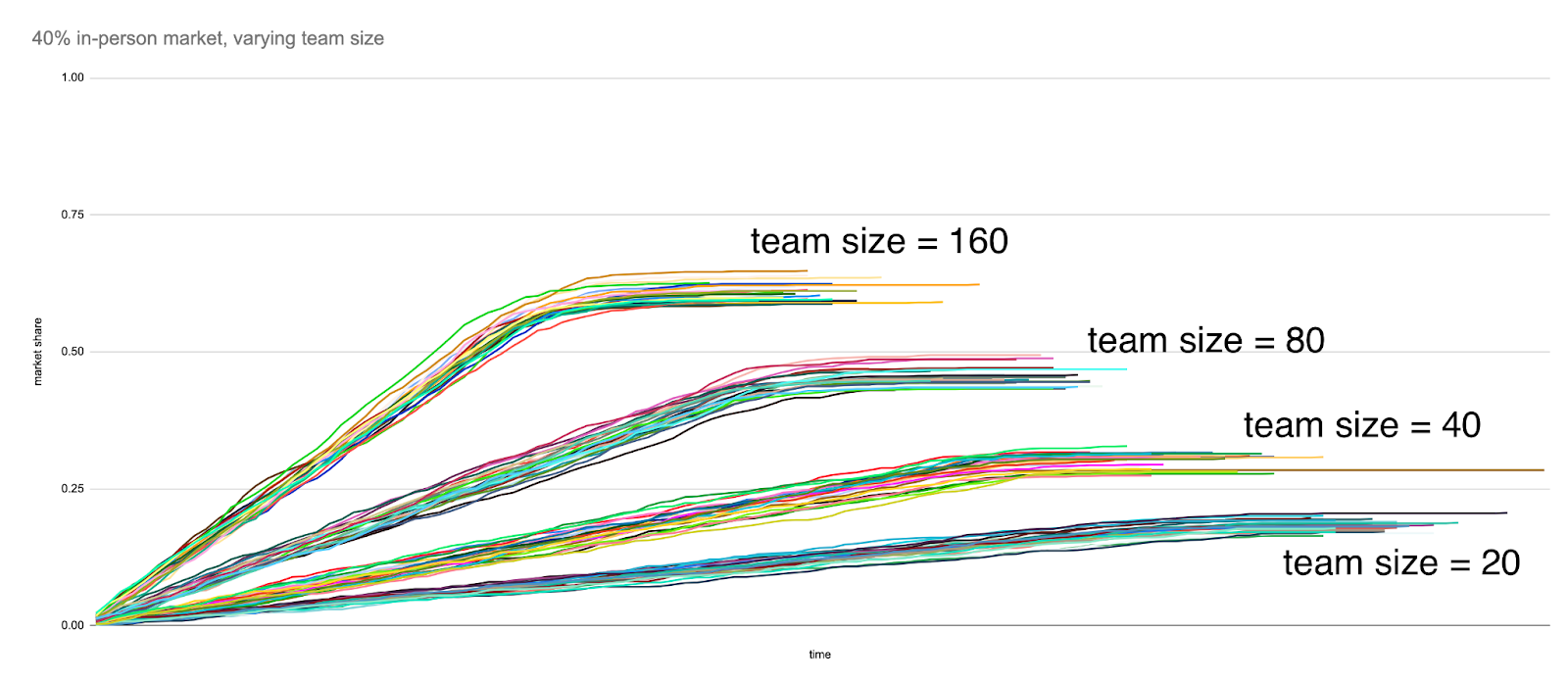
And again, the x-axis of each chart is a representation of time within each simulation, where a “tick” of the clock corresponds to each sales team replacing their current set of leads with new leads from the prospective customer base at random. The y-axis represents the in-person team’s market share at a given point in the simulation. When a line flattens out, that is an indication that a particular execution of a strategy (e.g. choosing to invest in in-person sales events to raise the in-person win rate from 0.1 to 0.2) has completed, and the eventual finishing y-value of that line corresponds, roughly, to a notion of “eventual market share”. The lines are grouped into clusters of 25 runs for a given in-person win rate.

While this analysis doesn’t take into account any notion of cost of revenue, you can see that there is a very direct relationship between the team size and eventual market share, that is eventually bound by the team size relative to the competition — if you keep growing the size of your sales team, either by hiring or making them more efficient, you will continue to capture market share. As expected, things are a little bit less straightforward with increasing the win rate for in-person deals only. While eventual market share increases steadily as in-person win-rate is increased from 0.1 to 0.2 to 0.4 for in-person sales, a sales team with an in-person win rate of 0.8 is still bound by the share of the market that is operating in person.

Here is the same simulation run for prospective customer base proportions equal to 60% and 90%, respectively:

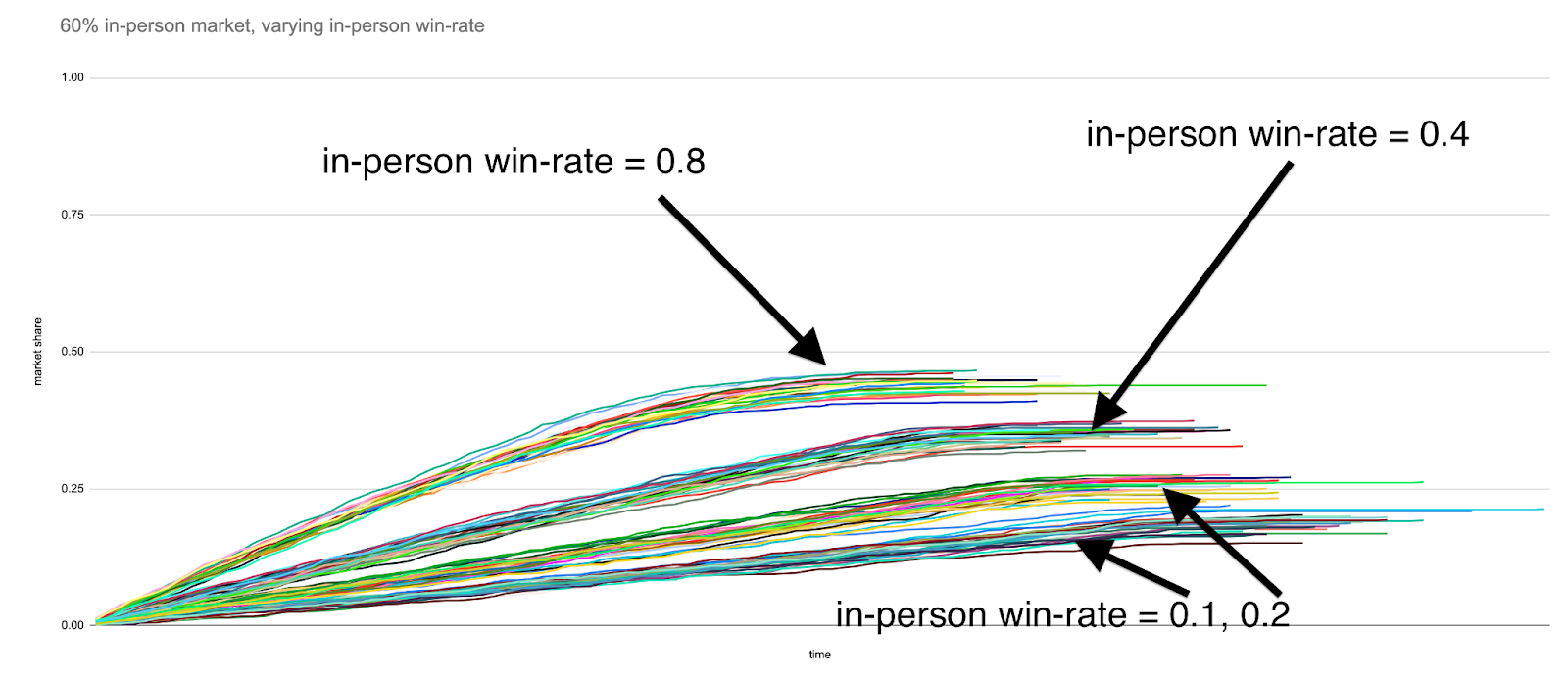
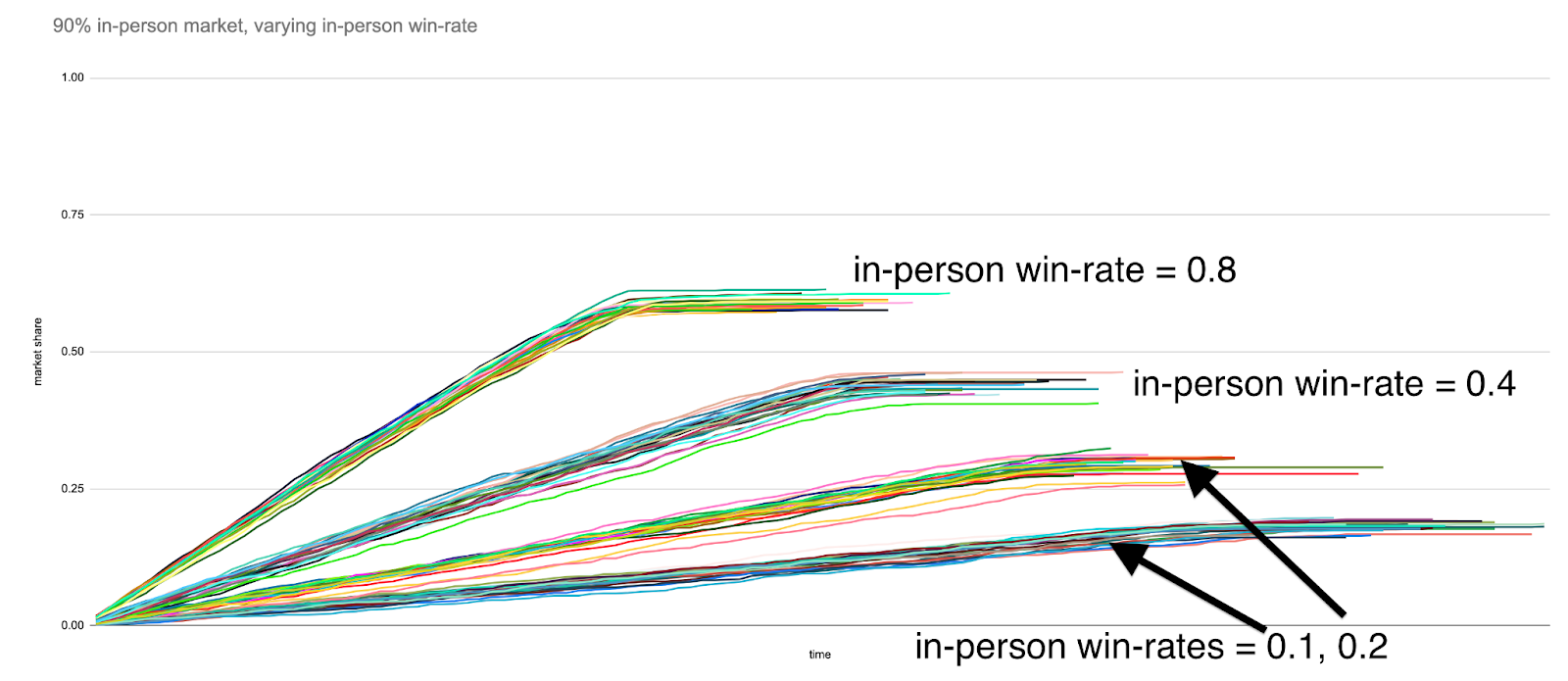
We see that investing in in-person strategies to boost win rate only start to perform as well as growing the sales team size once the market has approached pre-pandemic levels of in-person operation.

Conclusion

For firms that have a heavy external, customer-facing component to their operations, the decision to return to the office depends on an estimate of how quickly the world is going to transition back to in-person work. If you think that business travel is going to snap right back, then it perhaps makes sense to also invest in in-person events for your own sales team.

If, however, you are looking at the recent news about, for example, the delta variant, and think “hmm maybe we won’t be going back to huge 10,000 person sales conferences right away”, perhaps it makes more sense to invest in scaling out your sales team, either by hiring more, or investing in remote-work technology, or both.

If you are curious, here is the code used to run the above simulations.

Lately I’ve been thinking about what goes into a good campaign slogan, chant, or epithet. This post focuses on chants.

The Trump campaign birthed vastly more memorable chants than the Clinton campaign:

“Lock her up. Lock her up.”

“Build the wall. Build the wall.”

“Drain the swamp. Drain the swamp”

Despite following her campaign avidly and voting for her, I cannot recall a single chant from Hillary’s campaign. A quick perusal of “Hillary Clinton Campaign Chant” on google points to a far less impressive offering:

“U-S-A, U-S-A”

“I’m with her. I’m with her”

And the obvious: “Hill-a-ry, Hill-a-ry”.

I am positive that I heard these chants while watching the rallies, but I do not remember them.

What makes a chant memorable?

In the spirit of the set of rules cited in “Justin Timberlake Has a Cold” from Issue 20 of N+1 , I think it is worth writing down a few rules for composing a good, memorable chant. These are the tenets of chantability.

1.) An effective chant must contain fewer than 4 syllables.

It needs to fit into a 2 or 4-beat bar that is repeated. All of the chants listed above satisfy this criteria. Triple-meter chants are non-starters, for reasons that I hope are waltzingly obvious.

As an example of a chant that falls outside of Rule 1.), I can recall walking by a few rallies near the Trump tower in NYC. I could hear clearly the “Not My President” chant in action. Because this chant is 5 syllables long, it requires the added complexity of 2 repetitions before you can nod your head to it:

“Not – my – pres-i – dent, NotMy – Presi – Dent!”

(I have all intentions of writing this down on a staff consisting of 2 bars in 4/4 meter, but I hope you can get the sound of it — Pres-i is a dotted eigth/sixteenth type figure).

Don’t get me wrong — when I hear that chant, I want to get up and dance (and throw in a Lil Jon “WHAT?” at the end, or even “OKAYE!”). But this impulse is distracting from the message. The chant is too inventive, rhythmically. These protesters would have a stronger message if they had stuck to 2 or 3 syllables:

“Re – ject – Trump. (breath). Re – ject – Trump (Breath)” (4/4 bars, 3 syllables)

“Trump Sucks Trump Sucks Trump Sucks” (2/4 bars, 2 syllables).

Keeping the entire chant to 3 syllables or less allows it to bore deeper into our brains. Time dilutes every message.

2) An effective chant must contain a verb.

This is the primary place that Hillary’s chants fall short. “Hillary, Hillary, Hillary” is simple, but it has no action, no verb. The same goes for “USA, USA”.

Trump’s chants, on the other hand, employ very colorful verbs in spades* : “drain”, “lock”. You could even make the argument that the verbs are strong enough that they could fully signify their corresponding 3-syllable slogans ALONE, as single words:

“Drain! Drain! Drain! Drain”

“Lock! Lock! Lock!” (though this one is a bit weaker than “Drain”, in my opinion).

While “I’m with her” technically HAS a verb (to be), its strength is diluted by:

a). The fact that it is contracted into the WORST of all subjects, from a political perspective, “I”. Individuals don’t win elections. WE win elections by STAMPING OUT THE OTHER GUY.

b). The verb “to be”, which, as we’ve all been taught, is the root of all weak, passively-constructed evils in writing. Ick. “Hillary WAS accompanied by her supporters.” “The debates WERE won by Hillary.” “I AM supporting her.”

Here are some better chants:

“We – Want – Her.”

“Yank – the – Tou – pée”

“Fi – re – Trump”

3) An effective chant must employ vowel phonemes in a recognizable way.

This one is more complicated, but the general idea is that you want your chant to be somewhat recognizable even if all the consonants were stripped away. For instance, you could argue that the “Fire Trump” chant above would be better and more humorously shortened to the two-syllable “Dump Trump”. Chanting this in a crowd, however, is problematic. As was famously documented in the Simpsons, what people hear can depend heavily on the acoustics and the size of the crowd and/or what kind of microphone is being used to create the youtube video that gets uploaded. “Dump Trump” could easily become “Trump! Trump!”. Despite it missing a verb, “U-S-A” is a fantastic arena chant because it has only a single bona-fide consonant sound, and three distinct vowel sounds — “oo”, “eh”, and “ay” (as in “say”). This is probably the only criteria by which the Trump slogans fail, with “Build the Wall” being the most flagrant failure, combining three very similar vowel sounds.

I can’t think of one right now, but a slogan that employed the vowel sounds “ee”, “ah”, and “oo” in that order would be very effective, as the distance, phoneme-wise, between each successive vowel is enormous.

Perhaps “Pee – On – You” works? **

 

* Apologies.

** Apologies.

One of the ways that I get conversation started at a party is by asking everyone in a group what they think the maximum speed of a train on the MTA is on a given day. I’m not asking what the fastest train, on average is (most people say the A or the D between 59 and 125, with the token person or two advocating breathlessly for the Q, at least in the crowds I roll with). Rather, I am asking what the maximum value of dx/dt is in a 24 hour period across all trains. You’d be surprised at the responses I get. Most people will say something like “40 miles per hour”, or type “max train speed mta” into their phone which, with some diligent search result spellunking, will get you this site. That site, by the way, does not answer the question — it merely states the fastest speed ever attained by a NYC subway model car in history (87 mph), which occurred on some LIRR track, which technically is outside of the set of lines operated by the MTA.

My current guess is something near 60 miles per hour, on the A train in between 59th St and 125th. For the longest time, though, this was not my answer. I spent a number of years believing that the fastest speed you could hit on the MTA on a given day was between 72nd street and 42nd street on the 2 train, running express. I thought this for two reasons:

1. The MTA, between 2009 and 2010, spent a lot of time re-doing the tracks on the 2-3 express line in Manhattan, which I noticed because it would seriously hamper my commute from Washington Heights down to Union Square, where I worked. After it was done, I could have sworn that they had graded the tracks so that when the train made its gradual leftward bend between 66th street and 59th st., the subtle tilt in the track cancelled out whatever centripetal force there was, actually allowing you to ride “hands-free”, if you were crazy or enough of a hypochondriac to do so. Clearly the train was moving very quickly at this point.

2. This seemingly unnecessary investment in track infrastructure, combined with my acute awareness that most folks riding from 72nd street to 42nd street on the express line were fairly high-powered financier or lawyer types — these two legs of thought wishboned their way upward into an all-out conspiracy theory that the 2 train, from a train-infrastructure-financing perspective, effectively transformed itself into a “first-class” train precisely at the moment when the most wealthy, educated, and worldly passengers needed to ride it a single stop from their extremely large and clean apartments on the UWS down to their jobs atop the Bank of America tower. And what better way is there to tell every other passenger on the car that you have effectively subsidized most of the actual fare of $10/ride (or whatever number that is bandied around to justify fare hikes) that it costs for the MTA to haul their overweight and lazy asses to wherever the fuck in Brooklyn they are going, than by having that train, your train, PEAK THE FUCK OUT PRECISELY AT THE MOMENT YOU STEP ON WITH YOUR ITALIAN SUIT ON THE WAY TO YOUR EXTREMELY IMPORTANT OCCUPATION???

At that point in time, I was convinced that the 2 train was hitting 80 m.p.h. every morning.

I have since changed my views. One important realization came to me sometime in 2012, when I noticed that there were quite a few metal pillars flying by quite close to the 2-3 train’s windows during its rocket leg through midtown. Right around the same time, I noticed that the IRT-flavored 2 train (along with its extremely crowded sister trains on the 4-5 line) was an exceedingly narrow train when compared to the much more wide IND-flavored trains that ran on the ABCD lines. The walls of the stations that flew by on the 2 train were thus several yards closer than the walls on the more spacious 8th avenue express line. Could it be that my sense of velocity was skewed by my visual (not to mention socio-economic) perceptions? Did the 2-3 seem fast merely because of motion parallax?

Incidentally, I have tried and failed to test this theory. Many of my attempts to measure the time between stations on 2-3 line have been thwarted by train delays and/or difficulty determining the exact point where the stopwatch should be started/stopped. Plus, it might all be moot, as I have not had the delight of riding, say, the relatively more modern 4/5/6 trains into the northern reaches of the Bronx where the train stops are further apart, or the A train between Howard Beach and Broad Channel *.

Anyhow, I digress. People really get worked up about stuff like this at a party. For instance, a friend of mine was convinced that the C train (yes, the C train), was the fastest train in the MTA, and that it hit its peak velocity between HIgh Street and Fulton Street. When I pressed him further, he explained his theory that the C train was able to travel faster than the other trains because, as the oldest set of cars in the MTA’s fleet, most of its operational controls were left to manual efforts, including door operation, stop announcing, and applicably, the all important accelerator and (in the case of the C train)  lack of an automated velocity check. At this point, I really could have ripped his argument to shreds, having TIMED THAT VERY LEG of my new commute from brooklyn successfully  (it hits 35 mph, at best). Being at a social function, though, I eased up and sympathized with him, having enjoyed the extreme 2nd and 3rd derivatives of location with respect to time on the downtown C from 163 a number of times in years past. “It could happen”, I told him, as the C train most certainly takes the crown with respect to acceleration and “jerk” (yes, that’s the term for the third derivative of position with respect to time, or the rate at which the acceleration is increasing/decreasing), thanks to its exceedingly sensitive manual controls, and, from what I can tell, imbalanced operators **.

* http://web.mta.info/nyct/facts/ffsubway.htm There are more than 3 miles between these stations! There has GOT to be at least one day a week when an operator just FLOORS it, say, at mile 2.

** There was this one time where it was 9 AM and I was getting on the C at 168, and it was very obvious that the female operator of the train was having a tough morning, as she had all but lost it telling the you-know-whats in the back of the train to stop holding the goddamn door in the rear. Note that the 168 stop on the C very likely marked the first ride of a morning shift for her. Needless to say, when we got to 163, a mere 5 blocks south of 168 on the St. Nick diagonal, and those you-know-whats were still holding the doors in the rear of the train, presumably for purely recreational purposes, she got the f out of the train cockpit and took care of business, because that train really flew the rest of the way downtown that day.

 

How if, when I am laid into the tomb
I wake before the time that Romeo
Come to redeem me? there’s a fearful point!
Shall I not, then, be stifled in the vault,
To whose foul mouth no healthsome air breathes in,
And there die strangled ere my Romeo comes?

–from Shakespeare’s Romeo and Juliet

I wanted the second post in this series to be about distributed systems. A distributed system is any system in which computation is done on separate machines that communicate across a network. As I scanned the web for papers about distributed systems–particularly systems in which information flows across the network in an asynchronous way, I came upon Fischer, Lynch, and Paterson’s Impossibility of Distributed Consensus with One Faulty Process. The paper is short, and made for a quick read. It would be perfect for this month’s blog post, which was already quite overdue. I became interested, however, in another blog that had already done the work for this particular article — the Paper Trail is a great blog, and it has a great summary of the FLP result. I explored this blog and found a treasure trove of posts about other famous CS papers and discovered yet ANOTHER blog that actually paired Brewer’s CAP theorem with an account of a Sex Pistols concert.

Apparently, essays about distributed systems and music are pretty easy to come by.

Rather than duplicate work, I got to thinking about the small shred of the CS-paper universe that I had seen in this ego-slaying discovery of musical online compatriots in CS theory. There were a lot of fundamentally negative results. Turing’s result is negative in nature–a turning machine cannot decide if a given turing machine will be circle-free. The FLP impossibility result sparked a flurry of derivative papers, most of which were variations on a theme–finding some minimal set of constraints on a distributed system that would force consensus, or attempting to extend consensus impossibility to as broad of a swath of systems as possible. Either way, I could not help but feeling that there was something fundamentally negative about the universe that computer scientists could not escape.

Rather than pair this month’s seminal result, the FLP paper, with a work of music, I think it is more appropriate to pair it with a classic work of literature: Shakespeare’s Romeo and Juliet. This classic is arguably a rehashing of two other classics, Tristan and Isolde; and further back, Pyramus and Thisbe, but will do just fine for the present purpose of understanding the fundamental issue with distributed systems:  unreliable messengers.

In Romeo and Juliet, the final scenes see Juliet scheming with Friar Lawrence to free herself from the bonds of familial loyalty into true star-crossed-love via mock-death. The plan is to take a drug that will kill her for only two days–with the idea that two days should be more than enough time for her husband-to-be Paris to look elsewhere for a wife. A messenger, working for the Friar (a champion of true star-crossed love) will relay the true nature of the situation–FAKE DEATH–to Romeo, so that he can meet her when she wakes from the 48-hour coma.

Long, poetic story short, the messenger FAILS to deliver, Romeo finds Juliet overdosed, assumes her dead, kills himself, Juliet wakes, finds Romeo dead, kills herself, story over. What does any of this have to do with distributed systems?

As far as the mechanisms of the FLP result go, the key parallel in Shakespeare’s work is that the messenger fails to deliver. The message is super-important–that while Juliet LOOKS dead, she is actually alive. There is a reason why this tale of mistaken death is so timeless: DEAD vs. LIVE is as high as the stakes can get in terms of distributed systems and consensus. Granted, the authors of the FLP result make darn sure that the key process p that is adjacent to the the 0-valent and 1-valent initial configurations NEVER SENDS A MESSAGE in the key run of the system. The proof is a giant extension of the simple fact that that a single, faulty process can lie in between two different results of an admissible run. But it ultimately boils down to the fact that the messenger fails to inform. The subject of the message lives (Juliet), but the listening processes (Romeo) hear news of death, at precisely the wrong time (these moments occur infinitely often, in the system constructed by FLP). 

Is the FLP impossibility result really a significant result, given that literature holds hundreds, if not thousands of years of myths surrounding this, the ultimate failed message? The drama of the dead/live mistake has been endlessly optimized from Pyramus to Tristan to Romeo–authors are constantly searching for and finding audiences to WEEP over its truth.

Granted, Shakespeare and his anonymous predecessor authors never intended to prove anything in a rigorous way about asynchronous systems. They were merely trying to construct a great story.

I personally think that the plethora of fundamentally NEGATIVE results in distributed systems can be traced back to Gödel–that his proof revolving around the sentence “this sentence is not provable” is fundamentally a messenger problem. This is a bit tough to explain–the messenger here is hidden, in a way. With distributed systems, the messages are explicit–the messenger speaks about entities separate from himself–inconsistency is achieved very simply by messenger failure that gets propagated; indefinitely in FLP, fatally in Shakespeare. With Gödel, more nuance is required, but the key to proving incompleteness came with the ability of a sentence to say something about the system in which it resided–the formal system’s fundamental flaw is in its ability to talk about itself. No messenger is necessary–the system is its own messenger. The tragedy is embedded, inherent, unavoidable in the systems of Turing and Gödel.

Here are some links to awesome music:

Tchaikovsky

Prokofiev

Wagner

Trevor Smith and I are teaming up: this is our first offering in a series of monthly posts pairing interesting computer science articles with classical music.

Listen to this:  Gondwana by Tristan Murail

Read this:  On Computable Numbers by Alan Turing

Alan Turing’s On Computable Numbers, with an Application to the Entscheidungsproblem is a seminal paper. Anyone taking a CS undergraduate core will encounter the notion of computability and the halting problem. Further from the ivory tower, it is not difficult to find people who are near-giddy about Turing Completeness:

Breaking news: HTML + CSS3 is Turing Complete,

People looking for help developing a Turing machine in Microsoft Excel,

A Turing machine built using Legos,

and Brainfuck, a language whose website describes it as “an eight instruction Turing-Complete Programming Language”.

Turing’s name has become quite literally a “formal” stamp of approval in the computing world.

Beyond a few feeble mechanical attempts, computers did not exist in 1936, and Mr. Turing didn’t appear that excited about making one — he was interested in making Godel’s work on incompleteness comprehensible. That is, Turing wanted to intuitively construct a class of decision problems that could be proven undecidable. Turing could not tackle this without defining a notion of “computable”. His definition leaned heavily on a few notions that we would recognize today as common, but required a little more formal attention-to-detail back then:

Turing describes memory:

We may compare a man in the process of computing a real number to a machine which is only capable of a finite number of conditions q1, q2, …. qI; which will be called ” m-configurations”

and the idea of output:

… the subsequence of the symbols printed by it which are of the first kind will be called the sequence computed by the machine. The real number whose expression as a binary decimal is obtained by prefacing this sequence by a decimal point is called the number computed by the machine.

Academic language aside, the machine Turing is defining is simple. Simple like a paper and pen are simple; simple like the gestalt of piles and piles of modern integrated circuits that is DRAM is not. Turing calls this machine an “‘automatic-machine’ (or alpha-machine)”. The machine has the following properties:

a tape divided into squares

symbols that are on the squares

the scanned symbol (the rth symbol). Modern texts will likely refer to this as the symbol the ‘head’ is pointing to.

configuration: the current m-configuration and the current scanned symbol (qn, G(r))

But this paper is not without its difficulties, especially when approaching it today (ie: we found this paper to be very long, tedious and arduous).

One initial difficulty: having both completed somewhat standard undergraduate classes in formal computation theory, the initial choice of terminology by Turing of “Circle-free” and “Circular” was extremely confusing to our modern eyes. Most undergraduates approach Turing’s ideas in their coursework from the “halting problem” angle. What is initially confusing here is the following:

CIRCLE-FREE != HALTS

How can this be? Turing quickly skirts over the definition of a circle-free machine early on in the paper when he describes it as the following:

If a computing machine never writes down more than a finite number of symbols of the first kind, it will be called circular. Otherwise it is said to be circle-free. A machine will be circular if it reaches a configuration from which there is no possible move, or if it goes on moving, and possibly printing symbols of the second kind, but cannot print any more symbols of the first kind.

(p. 233)

Finite. This should be the same as a machine that “halts”, right?

No. Turing’s machines are built to write down numbers. These numbers are (somewhat sneakily) implied to be repeating binary decimals on page 232:

The real number whose expression as a binary decimal is obtained by prefacing this sequence by a decimal point is called the number computed by the machine

So we’re essentially talking about endlessly repeating floats–the kind of numbers that you get when you type in [1] [/] [3] on a calculator, except in binary. Numbers with bars over the top of the last digit: 0.33333333…. for example (0.010101010… in binary). In Turing’s paper, the machine that prints 0.010101010… is “circle-free”, meaning it encounters no “terminal difficulty” in computation if it can keep printing out the endless decimal representation without pausing indefinitely to calculate. By this definition, “finite” numbers such as 4, 5, and 6 would be circle-free numbers, because the machine would just print out a sequence of zeroes after the decimal point: 6.000000000…. “Halting” really has no place in his discussion — for if we took a machine that “did not halt” by the “halting problem definition”, it would print out, say, 6.000 and then wait for an indefinite amount of time before printing out the next zero.

Understanding the important concept of a circle-free machine is critical, even if your only goal in reading the Turing is to see Godel’s diagonalization “done simply” (see the argument on page 247 of the article, where he argues that the machine H is circular by suggesting an infinite loop).

Why the Murail?

We thought long and hard about this. The Murail represents a significant representative work of a genre, spectral music, that has significant parallels with the work of Turing. Spectral music is detailed well in this wikipedia article

The Murail, like the Turing, uses an intuitive language, completely divorced from the method-as-music ideal of serialism (about serial music). Gondwana is based entirely off of the first sounds you hear in the piece — it is the subsequent deconstruction that leads the listener down a path that is nearly always defined momentarily — “the next sound will be a little more interesting than the one you’re hearing right now, but will not break the continuity of what has already been heard.”

The work starts off very simply. The piece begins with 7-8 moments of repeated sound (see 0:12, 0:30, 0:46, 1:01, 1:15, 1:28, 1:38, 1:48, and then MAYBE [1:55, 2:01, 2:07, 2:13-2:40] in the link here), as easily understood derivations from a simple sonic idea. We had better remember this sound because, after about two and a half minutes, it becomes very clear that this work of music has ambitions beyond repetition.

Indeed, these events are like Turing’s “appeal to intuition” by Murail. There is no recognition of pattern possible without repetition. With the seven chime-strike chords, Murail is handing us a ball of yarn — we will need it to find our way home from the complicated, thorny walk in the woods that is the rest of the piece. There is not going to be a resounding return; no recapitulation here. Every time I hear the piece, I think of the opening of the Turing — the simple tone initially adopted by Turing could easily have been transcribed from a 1930s fireside-style radio broadcast, especially when contrasted with some of the machinations used later in the paper (which are not without their errata — see turing errata for more info).

Beyond the opening, the Murail begins to dig deep into the essence of sound. At roughly 8 minutes into the work, a hissing begins to become a main sonic feature. The connection to the beginning is simple — there is a brief, percussive sound at the beginning of the piece with a few strings playing, perhaps a maracca — there are lots of high partials in that sound. But it brings to mind an important question — a question that is at the heart of spectral music: what kind of music is happening in the parts of sound waves that we DON’T hear? What about all the extremely high partials that dogs can hear? Above, those, even? They exist. They have to. A sound wave can be encoded by a number. Large numbers exist. What if we slowed the noise, say, of water molecules at room temperature bouncing around inside a mason jar? Anyone that has been distracted by the sound of a tea kettle on the verge of boiling already knows that interesting sonic things can happen with water molecules on the surface of a boiling hotplate. But what about beyond the ear? What types of patterns exist at this sonic level of our world?

This is an interesting question that could use additional explanation. A strong argument can be made that much of “Western Harmony” can be boiled down into small, rational-number relationships between different frequencies. Numbers, in fact, that are easily computable by a Turing machine (with a reasonable “skeleton table,” even!). A major triad, for example, is little more than 1X, (5/4)X, (3/2)X (I, III, V). By the standards of Murail (and Turing, for that matter), these are small numbers, and the human ear is quite adept at doing the math of recognizing them and placing them in the context of “sounding good.” The human ear, from a perspective of what it can “understand” in this way, is quite good. We like minor chords, diminished chords, heck, we’ll even listen to Coltrane. Serial music is tougher. In general, music that doesn’t “sound good” to the western ear because of dissonance, etc. likely involves sound frequency relationships that make use of larger numbers. A minor chord, for example, requires use of the 6th and 8th partials. What is the limit? What is uncomputable for the human ear?

Note:
Parallels with music aside, readers not familiar with Turing’s life and the circumstances of his death should read this: turing wikipedia article. Oppression and intolerance are real, and Turing suffered greatly at the hands of the British government.